![]() ,
,
(2-4)
Hustotu zářivého toku v závislosti na teplotě objektu zkoumal rakouský fyzik Boltzmann. Došel k závěru, označovaném dnes jako Stefanův – Boltzmannův zákon, který říká:
Každé těleso, které má nenulovou absolutní teplotu září, přičemž hustota zářivého toku je úměrná čtvrté mocnině absolutní teploty.
Matematickou formulaci Stefanova – Boltzmannova zákona lze získat, provedeme-li integraci spektrální hustoty zářivého toku dokonale černého tělesa Eol dle Planckova vyzařovacího zákona, a to přes celý rozsah vlnových délek a za konstantní teploty. Pro hustotu zářivého toku dokonale černého tělesa dostaneme
|
|
(2-4) |
kde so je Stefanova - Boltzmannova konstanta, která má hodnotu so = 5,6697.10-8 W.m-2.K-4. Hustotu zářivého toku dokonale černého tělesa Eo lze zobrazit v diagramu závislosti spektrální hustoty zářivého toku dokonale černého tělesa Eol na vlnové délce l, viz obr. 2-4, jako plochu pod danou izotermou.
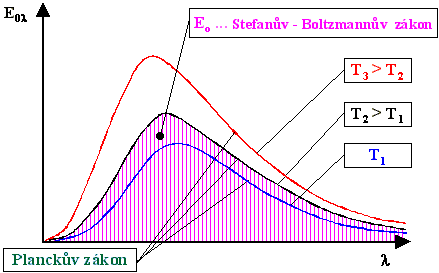
Obr. 2-4 Zobrazení Stefanova – Boltzmannova zákona v diagramu závislosti spektrální hustoty zářivého toku dokonale černého tělesa na vlnové délce záření
Pro nedokonalé zářiče, které se také označují jako šedé povrchy, lze pak hustotu zářivého toku vyjádřit vztahem
|
|
(2-5) |
kde e je emisivita (poměrná zářivost) zářiče. Emisivita, nebo také poměrná zářivost vyjadřuje schopnost zářiče vyzařovat. Dokonalé zářiče (dokonale černá tělesa) mají e = 1, nedokonalé zářiče (šedá tělesa) mají e Î (0, 1) a absolutně nedokonalé zářiče (bílá tělesa) mají e = 0. Hodnoty emisivit pro různé povrchy lze nalézt v různých tabulkách, nebo také v příloze P1 a příloze P2 těchto skript.